1. Introduction:
Heat Transfer is one of the most common unit operations in Process Industry. In an ideal situation one would want to achieve heat balance between the Source and Sink without any loss of heat energy to the atmosphere. Unfortunately the above cannot be achieved in absolute terms, even though an attempt can be made to control the Heat Transfer in such a way so as to limit the heat loss to atmosphere to a minimum by employing Insulating Material over the metallic surface exposed to atmosphere. Besides, there could be some other factors (e.g. condensation and subsequent freezing of moisture over the exposed surface) which may necessitate using Insulating Material depending upon the operating conditions of the System under question. The cost considerations do however prevail upon, in deciding the appropriate level of Insulation that would prove to be most effective from an overall angle.
2. Purpose:
The objectives of providing the Thermal Insulation can be summarized as follows:
- To prevent Heat Loss from hot surface.
- To prevent Heat Gain by the cold surface.
- To prevent condensation (and subsequently ice formation) on cold surface.
- To provide Personnel Protection against accidental contact of human body with hot metallic surface.
3. Heat Transfer Principle:
The Heat Loss in case of a hot insulated circular pipe takes place due to heat flow through the following 4 steps refer sketch (Figure-1) below
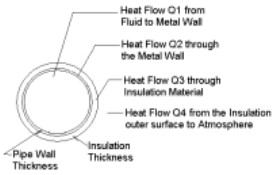
Fig 1 Thermal Insulation
Figure-1
1. Heat flow Q1 from fluid to inside surface of the metal wall by way of Convection
2. Heat flow Q2 across the metal wall by way of Conduction.
3. Heat flow Q3 across Insulation Layer by way of Conduction
4. Heat flow Q4 from the outer surface of metal wall to the atmosphere, predominantly by way of Convection.
Under steady state condition the rate of Heat Transfer through the above 4 steps will be same.
i.e. Q1 = Q2 = Q3 = Q4
In case of Heat Gain, by a cold insulated pipe the direction of heat flow will be opposite to that of the hot insulated pipe.
Rate of Heat Transfer by Conduction = K A * Δt = Δt / RCond
Where K = Thermal Conductivity
A = Surface Area
Δt = Temperature Gradient per Unit length
RCond (Thermal Resistivity due to conduction) = 1/ KA
Rate of Heat Transfer by Convection = h A *Δt = Δt / RConv
Where h = Convection Heat Transfer Coefficient
RConv (Thermal Resistivity due to Convection) = 1/ hA
ΔT = Differential temperature
Applying the above basis equations to the Insulated Pipe Cross Section and ignoring the thermal resistivity RConv and RCond for heat transfer in Step 1 and 2 (i.e. assuming that Step 1 and Step 2 practically offer no resistance to Heat Flow)
The Heat Loss across the Insulation
Q3 = K * 2πL * Δt1/ Ln (D2/ D1) _______________________ (Eq.1)
Where:
D2 = Outer Diameter of Insulation
D1 = Inner Diameter of Insulation
L = Length of Insulated Pipe
Δt1 = Temperature differential between inner and outer surface of Insulation.
The Heat Loss from Insulation Outer Surface to the Atmosphere
Q4 = h * πD2 L *Δt2 _______________________ (Eq. 2)
Where:
Δt2 = Temperature Differential t between the Insulation Outer surface and the Atmosphere.
Under steady state condition
Q3 = Q4
K * 2πL * Δt1/ Ln (D2/ D1) = h * DD2 L * Δt2
Conduction Heat Transfer Coefficient for Insulating Material K is typically 0.02 – 0.04 W/ m. OC
Convection Heat transfer Coefficient for Air (natural convection) is typically 15 – 20 W/ m2. OC
4. Determination Of Insulation Thickness:
The selection of Insulation Thickness is done based on 1 of the following cases for the given fluid and ambient temperature, wet bulb temperature (considered for cold insulation only) and wind speed (accounted for in the convection heat transfer coefficient for heat flow from insulation top surface to the atmosphere).
Case 1:
To maintain the temperature of the outer surface of the Insulation to a specified value from process angle i.e. for controlling the heat gain) in case of Cold Insulated Piping.
Case 2:
To maintain the temperature of the outer surface of Insulation above wet bulb temperature to avoid condensation and subsequent freezing of the atmospheric moisture in case of Cold Insulated Piping.
Case 3:
To maintain the temperature of the outer surface of Insulation from personnel Protection point of view in case of Hot Insulated Piping. A maximum temperature of 52 O C is considered to be acceptable.
Case 4:
To maintain the loss of Heat Energy to a specified value from the point of view of limiting the plant operating cost in case of Hot Insulated Piping. A value of 100 Kcal/ hr m2 is generally assumed to be satisfactory from the point of view of rationalizing the Annual Capital Investment vis-à-vis Annual Plant Operating Cost.
The calculation of Insulation Thickness for Cases 1 to 3 is done in following steps
Step 1: Assume an arbitrary Insulation Thickness.
Step 2: Determine Q4 based on the predetermined value of Δt2 (i.e. differential between the given temperature of outer surface of Insulation and the ambient) and the assumed value of Insulation Thickness in Step 1, as per equation (EQ .2)
Step 3: Equate Q3 = Q4
Step 4: For the value of Q3 arrived above, calculate the value of Insulation Thickness as per equation (Eq .1)
Step 5: Based on the calculated value of Insulation Thickness recalculate Q4
Step 6: Repeat Steps 3 to 5 until the value of Q3 and Q4 becomes practically same.
Step 7: Select the Insulation Thickness as calculated in Step 4 corresponding to the steady state achieved in Step 5.
The calculation of Insulation Thickness for case 1 is done on the similar principle as for case
1 to 3 with a minor variation in the approach, which is as follows
Step 1: same as above
Step 2 and Step 3: Not required since the Heat Loss (i.e. Q3 = Q4) is already specified.
Step 4: For the specified value of Q3 = Q4 calculate the value of Ät1 (i.e. temperature differential between the inner and outer surface of Insulation) based on the assumed value of Insulation Thickness in Step 1.
Step 5: Calculate the temperature of the outer surface of the Insulation based on the inner surface temperature as fluid temperature and Ät1 calculated in Step 4 above.
Step 6: Calculate Δt2 (i.e. differential between the calculated temperature of outer surface of Insulation in Step 5 above and for the given ambient temperature).
Step 7: Calculate Insulation Thickness based on Δt2 calculated above and the specified value of Q4.
Step 8: Repeat Steps 4 for the calculated value of Insulation Thickness in Step 7 above and specified value of Q3 = Q4 to arrive at a new value of Δt1
Step 9: Repeat Steps 5 to 7 to arrive at the new value of Insulation Thickness
Step 10: Repeat Steps 8 and 9 until a steady state condition is achieved (i.e. calculated
Insulation thickness in step 7 becomes constant)